首页

数据结构

散列表

两种解决碰撞的方法：拉链法和线性探测法。

拉链法：使用链表存储hash值相同的键。
- 查找：找到key所在的链表，从链表中顺序查找；
- 插入：找到key所在的链表，加入链表的头部；
- 删除：找到key所在的链表，从链表中删除。
线性探测法：使用空位来解决冲突，保证使用率在1/8至1/2之间。
- 查找：找到key所处的位置，未命中则线性向前查找，直到遇到空位，则判断为不存在；
- 插入：找到key所处的位置，如果冲突则线性向前探测到一个空位来存储冲突的键；
- 删除：删除该键，并顺序将当前键簇剩余所有键全部重新插入。

二叉查找树（BST）

一棵二叉查找树是一棵二叉树，且每个结点都大于其左子树的任一结点而小于其右子树的任一结点。

删除任意结点的流程：

为叶子结点直接删除；任一子结点为空，删除该结点，并将其父链接改为指向其非空的子结点。
若子结点均不为空，则找到该结点的后续结点，即其右子树的最小结点。
从右子树删除其后续结点，将后续结点的父链接改为指向后续结点的右子树（因为后续结点为树的最小结点，故其左结点必然为空）。
用后续结点替换掉该结点的位置。

平衡查找树

2-3查找树

一棵2-3查找树或为一棵空树或由以下结点组成：

2-结点，标准二叉查找树中的结点，含有一个键和两个链接
3-结点，含有两个键和三个链接

2-3查找树的插入操作

如果插入到2-结点上，直接组成一个3-结点即可；
如果插入到3-结点上，先组成一个临时4-结点，然后分裂成三个2-结点，将中间的结点移动到父结点中，并继续向上分解，直到不存在临时的4-结点或者到达了根节点。

红黑树

使用标准的二叉查找树（全部为2-结点）和一些额外信息表示一个2-3树，将一个3-结点替换为由一条左斜的红链接相连的两个2-结点，用黑链接表示结点之间的普通链接。

因为2-3树是完美平衡的（任意空链接到根结点的距离都相同），所以红黑树是完美黑色平衡的，任意空连接到根结点的路径上黑链接（黑色结点）数量都相同。

最坏情况下操作是2lgN级别（即左边路径全是3-结点），平均情况下所有操作均是lgN级别。

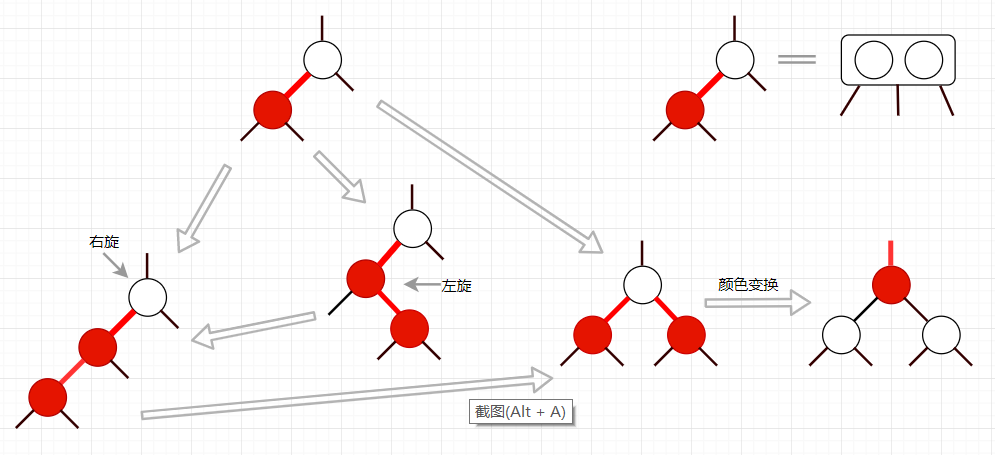
一、红黑树的插入操作

在沿着插入点到根路径向上移动的每个结点中完成以下操作即可实现插入：

如果左结点为黑色，右子结点为红色，进行左旋操作；
如果左子结点为红色且其左子结点也为红色，进行右旋操作；
如果左右子结点均为红色，进行颜色转换。

最后将根结点设为黑色。

二、自顶向下的2-3-4树的插入算法

2-3-4树允许存在4-结点，使用一条左斜的红链接和一条右斜的红链接以及三个2-结点来表示一个4-结点

插入算法要保证在向下查询路径上分解所有4-结点（通过颜色转换将一个4-结点变为3个2-结点），插入结点后向上回溯配平4-结点（通过旋转将不平衡的4-结点变成一条左斜和一条右斜组成的4-结点）。

相对于红黑树的插入算法，只需要将颜色转换的代码提前至空判断之后递归插入之前即可（即在插入结点前将4-结点配平，又因为可以存在4-结点所以插入的最后一步不再需要颜色转换）。

三、红黑树的删除最小值操作

删除最小值，沿着左链接向下过程中，保证不存在2-结点：

3个2-结点可以直接合并为一个4-结点；
如果兄弟结点不是2-结点，将兄弟结点最小键的移动到父结点中，将父结点的最小键移动到左子结点中；
如果兄弟结点也是2-结点，将左子结点、父结点最小键、兄弟结点合并成一个4-结点。

最后从3-结点或4-结点中删除最小值，然后向上回溯分解所有4-结点。

四、红黑树的删除操作

使用和删除最小值相同的变换保证向下查找路径中不存在2-结点，如果键在最底层直接删除即可，否则和二叉查找树一样，找到其后继结点，删去该结点并替换被删除结点即可。

五、Java红黑树实现

实现为2-3-4树，且每个结点均包含父结点的引用，同时允许单个右斜红链接存在。

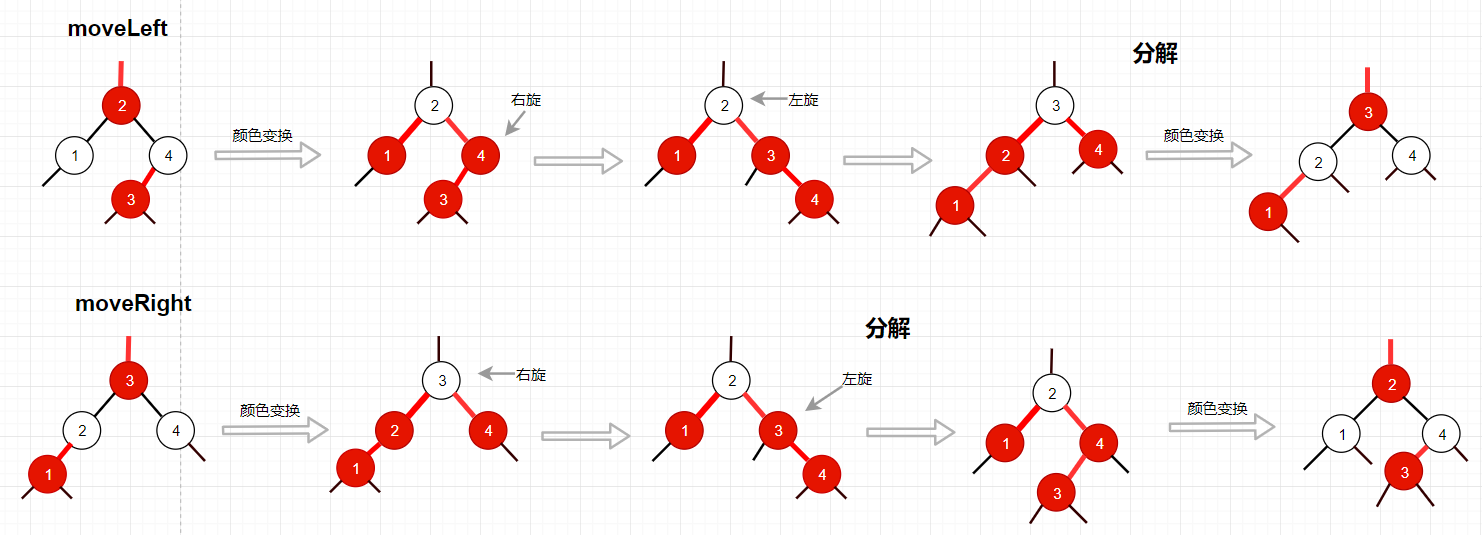
插入操作：新插入的结点都为红结点，自底向上配平4-结点，最多需要两次旋转以及多次颜色变换。
- 找到插入位置，父结点为黑色则直接插入成功，否则进入循环判断，直到父结点为黑色或者到达了根结点；
- 循环判断开始，如果父结点和叔叔结点均为红色，则直接颜色转换，当前结点设为爷爷结点，开始下一轮循环；
- 叔叔结点为黑色，则需要旋转爷爷结点，这之前需要通过旋转将当前结点倾斜方向与父结点调整为一致同时将当前结点与父结点交换，这个时候当前结点已被调整到爷爷结点的位置，继续下一轮循环；
- 循环结束后最后把根结点设为黑色。
删除操作：最多需要三次旋转以及多次颜色变换。
- 先查找被删除结点是否存在，不存在则直接结束；
- 如果存在左右子树，找到后继结点，即右子树的最小值，并用后继结点替换掉当前结点；
- 接下来删除当前结点，因为当前结点必然是只有一颗子树或者没有子树（如果使用后继结点替换过了，后继结点为最小值必然没有左子树），用空或存在的单棵子树替换其位置；
- 如果被删除的是黑结点则需要对兄弟结点进行调整（将兄弟子树路径上黑色链接数量减少1），自底向上直到恢复完美黑色平衡，循环判断直到当前结点不为黑结点。

图

无向图

非稠密无向图使用邻接表来表示，从图中任意一个顶点出发都存在一条路径到达另一个任意顶点，则此图是连通的。

有向图

一个顶点的出度为由该顶点指出的边的总数，一个顶点的入度为指向该顶点的边的总数。有向图中由顶点v能到达顶点w并不意味着由顶点w也能到达顶点v。

拓扑排序

给定一幅有向图，将所有顶点排序，使得所有的有向边均从排在前面的元素指向后面的元素。有向无环图才有拓扑排序，为所有顶点的逆后序排列。

计算有向图强连通分量的Kosaraju算法

1. 求得有向图的反向图的逆后序排列；
2. 按照上一步得到的排列顺序在有向图中进行深度优先搜索。

最小生成树

图的生成树是它的一棵含有所有顶点的无环连通子图，而加权无向图的最小生成树是它的一棵权值之和最小的生成树。

树的重要性质：
- 边的总数为顶点数减去1
- 用一条边连接任意两个顶点会产生一个新的环
- 从树中删去一条边将会得到两棵独立的树

贪心算法

根据切分定理，找到一种切分，它的横切边均不为黑色，则将它的权重最小的横切边标记为黑色，重复，直到标记了V-1条边为止。

切分定理

一幅加权图中，给定任意切分，该切分的横切边中权重最小者必然属于图的最小生成树。

切分：将图的所有顶点分为两个非空且不重叠的集合。
横切边：连接属于两个不同集合的顶点的边。

Prim算法

每一步都为一棵生长中的树添加一条边，一开始这颗树只有一个顶点，每次都将下一条连接树中的顶点与不在树中的顶点且权重最小的边加入树中，直到树含有V-1条边。

Kruskal算法

按边的权重顺序，将边加入最小生成树中，加入的边不与已加入的边构成环，直到树含有V-1条边。

最短路径树

从一幅加权有向图其中一个顶点出发的最短路径图是该图的一幅子图，它包含了顶点到所有可达顶点的最短路径。

边的松弛

放松边v->w意味着检查从s到w的最短路径是否是先从s到v再从v到w。

Dijkstra算法

权重非负的情况下，依次将当前距离起点最近的非最短路径树顶点放松并加入树，直到所有顶点都在树中。

拓扑顺序算法

无环情况下，按照拓扑顺序放松顶点，能在线性时间（E+V）内解决问题，为最优解法且与权重是否非负无关。

因为每个顶点在加入树后，其最短路径就已经被确定，这个顶点再也不会被放松，因为拓扑顺序下后面的顶点不存在指向它的边，
求得最长路径只需将权重全部取相反数即可。

Bellman-Ford算法

在任意含有V个顶点的加权有向图中给定起点s，从s出发无法到达任何负权重环，将distTo[s]初始化为0，其他初始化为无穷大，以任意顺序放松所有边V轮即可求最短路径树。

可用于查找负权重环，经过多轮放松后，负权重环必然会存在edgeTo[]构成的子图中。

关键路径

创建一幅无环有向加权图，包含一个起点s和一个终点t且每个任务对应着两个顶点（一个起点一个终点）。每个任务都有一条从它的起点到它的终点的且权重为任务所需时间的边。每条优先级限制v->w，都有一条从v任务终点到w任务起点且权重为0的边。没有前置限制的任务需要添加一条从s到任务起点且权重为0的边，没有后置限制的任务需要添加一条任务终点到t且权重为0的边。这样每个任务的开始时间为从起点到任务起点的最长距离，任务的关键路径为从s到t的最长路径。

字符串

三向字符串快速排序

三向快速排序和高位优先排序的结合，适合于含有较长公共前缀的字符串。相比于直接使用三向快速排序能显著的减少字符比较次数，而相比于普通的高位优先排序能避免产生大量的空子数组。

private static int charAt(String s, int d){
    if (d < s.length()) {
        return s.charAt(d);
    } else {
        return -1;
    }
}

private static void sort(String[] arr, int lo, int hi, int d){
    if (hi <= lo){
        return;
    }
    int v = charAt(arr[lo], d);
    int lt = lo, i = lo + 1, gt = hi;
    while (i <= gt) {
        int cmp = charAt(a[i], d) - v;
        if (cmp < 0) {
            swap(arr, i++, lt++);
        } else if (cmp > 0) {
            swap(arr, i, gt--);
        } else {
            i++;
        }
    }
    sort(arr, lo, lt - 1, d);
    // 等于区间还需要继续比较下一个位置的字符
    if (v > 0) {
        sort(arr, lt, gt, d + 1)
    }
    sort(arr, gt + 1, hi, d);
}

单词查找树

R向单词查找树

R向单词查找树，R为字符表的大小，每个结点都有R条链接，其中大量的链接可能都为空，每条链接对应一个字符。

三向单词查找树

三向单词查找树中，每个结点都含有一个字符、三条链接和一个值，三条链接分别对应当前字母小于、等于和大于结点字母的所有键。